7.8 Applications to Differential Geometry, Physics, and Forms of Life

footnote #In the first half of the nineteenth century, the great German mathematician Karl Friedrich Gauss developed a theory of curved surfaces in \({\mathbb{R}}^{3}\). More than a century earlier, Isaac Newton had defined a measure of the curvature of a space curve, and Gauss was able to find extensions of this idea of curvature that would apply to surfaces. In so doing, Gauss made several remarkable discoveries.

Curvature of Surfaces

For paths \({\bf c}{:}\, [a, b] \to \mathbb{R}^{3}\) that have unit speed—that is, \(\| {\bf c}^\prime (t)\| = 1\)—the curvature \(\kappa\) of the image curve \(\kappa ({\bf c}(t))\) at the point \({\bf c}(t)\) is defined to be the length of the acceleration vector. That is, \(\| {\bf c}^{\prime\prime}(t)\| =\kappa ({\bf c}(t))\). For paths \({\bf c}\) in space, the curvature is a true measure of the curvature of the geometric image curve \(C\). As we saw at the end of Section 7.2, the “total curvature” \(\int\kappa\, {\it ds}\) over \(C\) has “topological” implications.

The same, and even more, will hold for Gauss’ definition of the total curvature of a surface. We begin with some definitions.

Let \({\Phi}{:}\, D \to \mathbb{R}^{3}\) be a smooth parametrized surface. Then, as we know, \[ {\bf T}_u = \frac{\partial {\Phi}}{\partial u} \qquad\hbox{and} \qquad {\bf T}_v = \frac{\partial \Phi}{\partial v} \] are tangent vectors to the image surface \(S = {\Phi } (D)\) at the point \({\Phi } (u, v)\). We will also assume that there is a well-defined normal vector; that is, we assume the surface is regular: \({\bf T}_{u} \times {\bf T}_{v}\,{\ne}{\bf 0}\).

Let \[ E= \left\|\frac{\partial {\Phi}}{\partial u}\right\|^2, \qquad F= \frac{\partial {\Phi}}{\partial u} \ {\cdot} \ \frac{\partial {\Phi}}{\partial v},\qquad G = \left\|\frac{\partial {\Phi}}{\partial v}\right\|^2. \]

In Exercise 23 of Section 7.6, we saw that \[ \|{\bf T}_u \times {\bf T}_v\|^2 = EG - F^2. \]

For notational reasons, we denote EG – \(F^{2}\) by \(W\). Furthermore, we let \[ {\bf N} = \frac{{\bf T}_u \times {\bf T}_v}{\|{\bf T}_u \times {\bf T}_v\|} = \frac{{\bf T}_u \times {\bf T}_v}{\sqrt{W}} \] denote the unit normal vector to the image surface at \(p = {\Phi}(u, v)\). Next we will define two new measures of the curvature of a surface at \(p\)—the “Gauss curvature,” \(K(p)\), and the “mean curvature,” \(H(p)\). Both of these curvatures have deep connections to the curvature of space curves, which illuminate the meaning of their definitions, but we do not explore these here.

To define these two curvatures, we first define three new functions \(\ell, m, n\) on \(S\) as follows: \begin{equation*} \ell(p) = {\bf N}(u, v) \,{\cdot}\,\frac{\partial^2 {\Phi}}{\partial u^2} = {\bf N} (u, v) \,{\cdot}\, {\Phi}_{uu}\\[5pt] m (p) = {\bf N}(u, v) \,{\cdot}\,\frac{\partial^2 {\Phi}}{\partial u \partial v } = {\bf N} (u, v) \,{\cdot}\, {\Phi}_{uv}\\[5pt] n(p) = {\bf N}(u, v) \,{\cdot}\,\frac{\partial^2 {\Phi}}{\partial v^2} = {\bf N} (u, v) \,{\cdot}\, {\Phi}_{vv}.\tag{1} \end{equation*}

The Gauss curvature \(K(p)\) of \(S\) at \(p\) is given by \begin{equation*} K (p) = \frac{\ell n- m^2}{W},\tag{2} \end{equation*} and the mean curvature \(H(p)\) of \(S\) at \(p\) is defined byfootnote # \begin{equation*} H (p) = \frac{G\ell + En - 2 Fm}{2W},\tag{3} \end{equation*} where the right-hand sides of both expressions are calculated at the point \(p = {\Phi}(u, v)\).

Surfaces of Constant Curvature

Surfaces of constant Gauss and mean curvature are of great interest to mathematicians. It was known in the nineteenth century that the only closed and bounded smooth surfaces with “no boundary” and with constant Gauss curvature were spheres. In the twentieth century, the Russian mathematician Alexandrov showed that the only closed and bounded smooth surfaces without a boundary that do not intersect themselves and that have constant mean curvature must also be spheres. Mathematicians believed that Alexandrov’s result held even if the surface was allowed to intersect itself, but no one could find a proof. In 1984, Professor Henry Wente (Toledo, Ohio) startled the world by finding a self-intersecting torus of constant mean curvature.

Surfaces of constant mean curvature are physically relevant and occur throughout nature. Soap bubble formations have constant nonzero mean curvature (see Figure 7.52), and soap film formations (containing no air) have constant mean curvature zero (see Figure 7.53 and Figure 7.54).

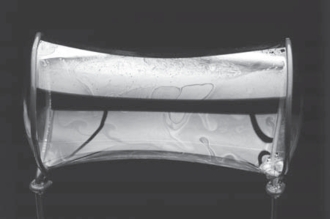
In the early nineteenth century, the French mathematician Delaunay discovered all surfaces of revolution that have constant mean curvature: the cylinder, sphere, catenoid, unduloid, and nodoid. The catenoid exists as a soap film surface spanning two circular contours.

Optimal Shapes in Nature

Throughout the ages, people have speculated on why things are shaped the way they are. Why are the earth and the stars “round” and not cubical? Why are life forms shaped the way they are?

In 1917, the British natural philosopher D'Arcy Thompson published a provocative work entitled On Growth and Form, in which he investigated the forces behind the creation of living forms in nature. He wrote:

In an organism, great or small, it is not merely the nature of the motions of the living substance which we must interpret in terms of force (according to kinetics), but also the conformation of the organism itself, whose permanence or equilibrium is explained by the interaction or balance of forces, as described in statics.

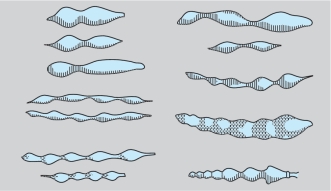
Surprisingly, Thompson discovered all of Delaunay’s surfaces in the form of unicellular organisms (see Figure 7.55). The constant mean curvature of these organisms can be explained by minimum principles similar to those described in the Historical Note in Section 3.3. In 1952, Watson and Crick determined that the structure of DNA is that of a double helix, a discovery that set the stage for the genetic revolution. We know from soap films, as in Figure 7.53, that nature likes helicoid forms, and nature tends to repeat patterns. A better understanding of the scientific principles underlying life may ultimately help mathematics play a more prominent role in this area of theoretical biology.

Curvature and Physics

The theory of curved surfaces, initiated by Gauss, has had a profound effect on physics. Gauss realized that the Gauss curvature K of a surface depended only on the measure of distance on the surface itself; that is, curvature was intrinsic to the surface. This is not true of the mean curvature \({H}\). Thus, beings “living” on the surface would be able to tell that the surface was curving, without any reference to an “external” world. Gauss himself found this mathematical result to be so striking that he named it theorema egregium, or “remarkable theorem.” Gauss’ theory was generalized by his student Bernhard Riemann to \(n\)-dimensional surfaces for which one could describe a notion of curvature.

Recall that Newton created the idea of a gravitational force acting over vast galactic distances, pulling galaxies together as well as pushing them apart (see Figure 7.56). In the early 1900s, Albert Einstein used Riemann’s ideas to develop the general theory of relativity, a theory of gravitation that eliminated the need to consider forces (as Newton did) acting over great distances. Einstein’s theory explained the bending of light by the sun, black holes, the expansion of the universe, the formation of galaxies, and the Big Bang itself. For most applications, including the dynamics of our solar system, Newton’s theory suffices and is commonly used today by NASA to plan space missions, as we saw in Section 4.1. But for cosmological applications on the grand scale, Einstein’s theory replaced that of Isaac Newton, published in his Principia in 1687.

As a testament to his genius, and despite the astounding success of this theory, Newton was nevertheless disturbed by questions about how this gravitational force acted. He could give no other explanation than to say, “I have not been able to deduce from phenomena the reason for these properties of gravitation, and I do not invent hypotheses; for anything which cannot be deduced from phenomena should be called an hypothesis.” Moreover, in a letter to his friend, Richard Bentley, Newton wrote:

That gravity should be innate, inherent and essential to matter, so that one body may act upon another at a distance, through which their action may be conveyed from one to another, is to me so great an absurdity that I believe no man, who has in philosophical matters a competent faculty of thinking, can ever fall into it.

Newton coined the term action at a distance (which means “force acting at a distance”) to describe the mysterious effect of gravitation over large distances. This effect is as difficult to understand today as it was in Newton’s time.

Johann Bernoulli found it difficult to believe in the concept of a force that acts through a vacuum of space over distances of even hundreds of millions of miles. He viewed this force as a concept revolting to minds unaccustomed to accepting any principle in physics, save those that are incontestable and evident. Additionally, Leibniz considered gravitation to be an incorporeal and inexplicable power, philosophically void.

It was perhaps Albert Einstein’s greatest inspiration (see Figure 7.57) to replace Newton’s model of gravitation with a model that would have thrilled the early Greeks—a geometric model of gravitation. In Einstein’s theory, the concept of a force acting through great distances has been replaced by the curvature of a space–timefootnote # world. As the quote at the beginning of the chapter illustrates, W. K. Clifford had a premonition of events to come! In order to elucidate Einstein’s scheme, we shall present an oversimplified model that conveys some of his basic ideas.

We represent space by a surface that we imagine as an originally flat trampoline (the vacuum state), which is at some point strongly deformed by the weight of a gigantic steel ball (the sun). A tiny steel ball rolling on the trampoline is our planet Earth (see Figure 7.58)

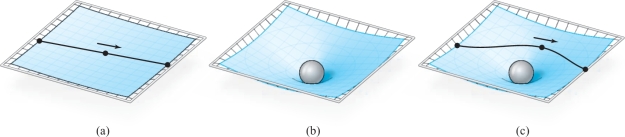
If we roll the small steel ball across the flat trampoline, it will travel in a straight-line path. However, if we now place the gigantic steel ball in the center, it will cause the trampoline to bend, or “curve,” even “far away” from the large ball. If we then give our little ball a push, it will no longer travel in a straight line but in a curved path. The big ball affects the trajectory of the little ball by curving the space around it. With just the right push, the little ball might even orbit the big one for a while. This trampoline model explains how a large body could, by curving space, influence a small one over great distance.

Einstein stated that space–time is curved by matter and energy. In this curved space–time, even light rays are bent as they pass near massive objects like our sun. Thanks to Gauss and Riemann, the curvature of space–time requires no external “universe” in which it curves. Moreover, in Einstein’s curved world, light travels along shortest paths in space–time called geodesics. It is normally impossible to observe light rays close to the bright Sun, but a solar eclipse provides a marvelous opportunity for such measurements. Two British expeditions to New Guinea (under Eddington and Cottingham) and to Sobral in northern Brazil used the solar eclipse of May 29, 1919, to observe whether light rays coming from stars and passing close to the Sun were bent. Both expeditions were able to confirm Einstein’s prediction, and Eddington later wrote,

Oh leave the Wise our measures to collate;

One thing, at least, is certain: LIGHT has WEIGHT.

One thing is certain, and the rest debate:

Light-rays, when near the Sun, DO NOT GO STRAIGHT.

The equations that tell one how much space and time are curved by matter and energy are known as Einstein’s field equations. A description of them is beyond the scope of this book, but the mathematical kernel from which these equations arise is not; this kernel is based on another remarkable result of the research of Gauss and Bonnet.

Gauss–Bonnet Theorem

In Example 2, we computed the Gauss curvature \(K\) of the sphere \(x^{2}+y^{2}+z^{2}=R^{2}\) of radius \(R\) and found it to be the constant 1\(/R^{2}\). The Gauss curvature \(K\) is a scalar-valued function over the surface, and as such we can integrate it over the surface. We wish to consider a constant times this surface integral, namely, \[ \frac{1}{2\pi}\int\!\!\!\int\nolimits_S K \ {\it dA}. \]

For the sphere of radius \(R\), this quantity becomes \[ \frac{1}{2\pi R^2} \int\!\!\!\int\nolimits_S \ {\it dA} = \frac{4\pi R^2}{2\pi R^2} =2. \]

What Gauss and Bonnet discovered was that if \(S\) is any “sphere-like” closed surface (closed and bounded, but with no boundary, as in Figure 7.59), then \[ \frac{1}{2\pi} \int\!\!\!\int\nolimits_S K\ {\it dA} =2 \] still holds.footnote #

Thus, the integral \[ \frac{1}{2\pi}\int\!\!\!\int\nolimits_S \ K \ {\it dA} \] always equals the integer 2, and is therefore a topological invariant of the surface. That the integral of curvature should be an interesting quantity should be already clear from the discussion at the end of Section 7.2.

Now consider a torus, or doughnut. The torus can be considered as coming from the sphere by cutting out two discs and gluing in a handle (see Figure 7.60).

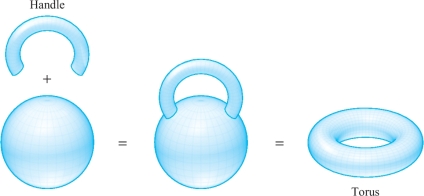
Moreover, we can continue this process adding 1, 2, 3, \(\ldots , g\) handles to the sphere. If \(g\) handles are attached, we call the resulting surface a surface of genus \(g\), as in Figure 7.61. Notice that the torus has genus 1.

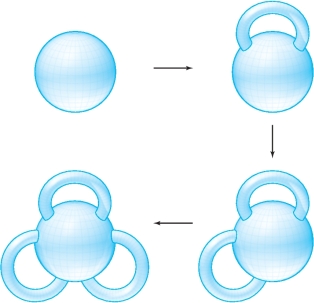
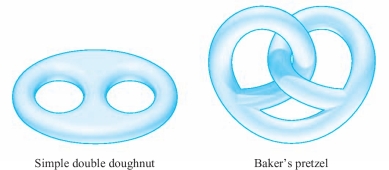
If two surfaces have a different genus, they are topologically distinct, and thus cannot be obtained from one another by bending or stretching. Interestingly, even two surfaces with the same genus can sit in space in quite different and complex ways, as in Figure 7.62. Astonishingly, even though the integral (or total curvature) given by \((1/2\pi)\int\!\!\int_{S} {\it K dA}\) depends on the genus, it does not depend on how the surface sits in space (and thus not on \(K)\).

Gauss and Bonnet proved that \[ \frac{1}{2\pi} \int\!\!\!\int\nolimits_S \ K \ {\it dA} = 2 -2g. \]

Thus, for the sphere (\(g = 0\)), it is always 2 (already verified); for the torus, it is always 0 (see Exercise 10).

There is something even more remarkable connected to the theorem of Gauss–Bonnet, observed by the great German mathematician David Hilbert (Figure 7.63).

Hilbert observed that the Gauss–Bonnet theorem is, in effect, a two-dimensional version of Einstein’s field equations. In the physics literature, this fact is known as Hilbert’s action principle in general relativity.footnote # Not surprisingly, similar geometric ideas are being employed by contemporary researchers in an effort to unify gravity and quantum mechanics—to “quantize” gravity, so to speak.